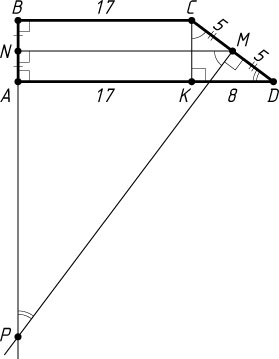
2019. В прямоугольной трапеции основания равны 17 и 25, а большая боковая сторона равна 10. Через середину M
этой стороны проведён к ней перпендикуляр, пересекающий продолжение второй боковой стороны в точке P
. Найдите MP
.
Ответ. 35.
Указание. Проведите среднюю линию трапеции и рассмотрите подобные треугольники.
Решение. Пусть N
— середина меньшей боковой стороны AB
трапеции ABCD
, K
— проекция вершины C
меньшего основания BC
на большее основание AD
. По теореме Пифагора
CK=\sqrt{CD^{2}-KD^{2}}=\sqrt{CD^{2}-(AD-AK)^{2}}=
=\sqrt{CD^{2}-(AD-BC)^{2}}=\sqrt{10^{2}-8^{2}}=6.
Из подобия треугольников NMP
и KCD
(по двум углам) находим, что \frac{MN}{CK}=\frac{PM}{CD}
. Поэтому PM=\frac{MN\cdot CD}{CK}
. Поскольку MN=\frac{1}{2}(AD+BC)
(средняя линия трапеции), то
PM=\frac{21\cdot10}{6}=35.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 61 с. 60
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.11, с. 112
