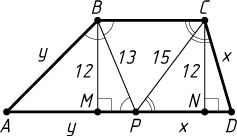
2020. Биссектрисы тупых углов при основании трапеции пересекаются на другом её основании. Найдите стороны трапеции, если её высота равна 12, а длины биссектрис равны 15 и 13.
Ответ. 14; 12,5; 29,4; 16,9.
Указание. Указанные биссектрисы отсекают от трапеции равнобедренные треугольники.
Решение. Пусть биссектрисы тупых углов B
и C
пересекаются в точке P
, принадлежащей большему основанию AD
трапеции ABCD
. Тогда \angle APB=\angle PBC=\angle PBA
, значит, треугольник ABP
— равнобедренный. Аналогично, треугольник PCD
— также равнобедренный.
Обозначим CD=DP=x
, AB=AP=y
, M
и N
— основания перпендикуляров, опущенных из вершин соответственно B
и C
на AD
. Тогда
PN=\sqrt{15^{2}-12^{2}}=9,~PM=\sqrt{13^{2}-12^{2}}=5.
Следовательно, BC=MN=PM+PN=5+9=14
.
По теореме Пифагора
PC^{2}-PN^{2}=CD^{2}-DN^{2},~15^{2}-9^{2}=x^{2}-(x-9)^{2}.
Отсюда находим, что x=12{,}5
. Аналогично,
PB^{2}-PM^{2}=AB^{2}-AM^{2},~13^{2}-5^{2}=y^{2}-(y-5)^{2}.
Отсюда находим, что y=16{,}9
. Следовательно,
AB=y=16{,}9,~CD=x=12{,}5,~AD=AP+PD=y+x=29{,}4.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.198, с. 171
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.24, с. 31
