2029. Двойное отношение четырёх точек. Даны две прямые l
, l_{1}
и точка O
, не лежащая ни на одной из них. Четыре прямые, проходящие через точку O
, пересекают прямую l
в точках A
, B
, C
и D
, а прямую l_{1}
— в точках A_{1}
, B_{1}
, C_{1}
и D_{1}
соответственно. Докажите, что \frac{AC}{CB}:\frac{AD}{DB}=\frac{A_{1}C_{1}}{C_{1}B_{1}}:\frac{A_{1}D_{1}}{D_{1}B_{1}}
.
Указание. Через точки B
и B_{1}
проведите прямые, параллельные прямой OA
, или примените метод площадей.
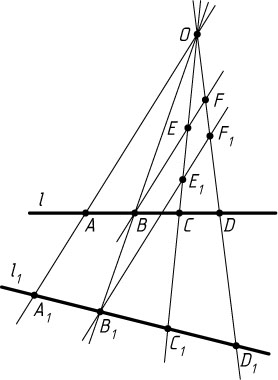
Решение. Первый способ. Пусть прямая, проходящая через точку B
параллельно OA
, пересекает прямые OC
и OD
в точках E
и F
соответственно, а прямая, проходящая через точку B_{1}
параллельно OA
, пересекает прямые OC
и OD
в точках E_{1}
и F_{1}
соответственно.
Из подобия треугольников AOC
и BEC
следует, что \frac{AC}{CB}=\frac{OA}{BE}
, а из подобия треугольников AOD
и BFD
— \frac{AD}{DB}=\frac{OA}{BF}
. Разделив первое из этих равенств на второе, получим, что
\frac{AC}{CB}:\frac{AD}{DB}=\frac{BF}{BE}.
Аналогично
\frac{A_{1}C_{1}}{C_{1}B_{1}}=\frac{OA_{1}}{B_{1}E_{1}},~~\frac{A_{1}D_{1}}{D_{1}B_{1}}=\frac{OA_{1}}{B_{1}F_{1}},~~\frac{A_{1}C_{1}}{C_{1}B_{1}}:\frac{A_{1}D_{1}}{D_{1}B_{1}}=\frac{B_{1}F_{1}}{B_{1}E_{1}},
а так как \frac{BF}{BE}=\frac{B_{1}F_{1}}{B_{1}E_{1}}
, то
\frac{AC}{CB}:\frac{AD}{DB}=\frac{A_{1}C_{1}}{C_{1}B_{1}}:\frac{A_{1}D_{1}}{D_{1}B_{1}}.
Что и требовалось доказать.
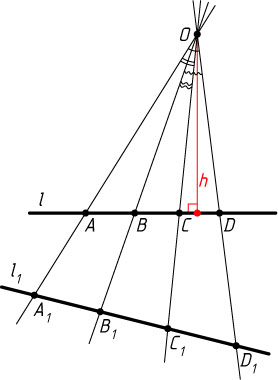
Второй способ. Пусть h
— расстояние от точки O
до прямой l
. Тогда
S_{\triangle AOC}=\frac{1}{2}AC\cdot h=\frac{1}{2}OA\cdot OC\sin\angle AOC,
S_{\triangle BOC}=\frac{1}{2}BC\cdot h=\frac{1}{2}OB\cdot OC\sin\angle BOC,
S_{\triangle AOD}=\frac{1}{2}AD\cdot h=\frac{1}{2}OA\cdot OD\sin\angle AOD,
S_{\triangle BOD}=\frac{1}{2}BD\cdot h=\frac{1}{2}OB\cdot OD\sin\angle BOD.
Откуда
AC=\frac{OA\cdot OC\sin\angle AOC}{h},~BC=\frac{OB\cdot OC\sin\angle BOC}{h},
AD=\frac{OA\cdot OD\sin\angle AOD}{h},~BD=\frac{OB\cdot OD\sin\angle BOD}{h}.
Следовательно,
\frac{AC}{CB}:\frac{AD}{DB}=\frac{AC\cdot DB}{CB\cdot AD}=\frac{\frac{OA\cdot OC\sin\angle AOC}{h}\cdot\frac{OB\cdot OD\sin\angle BOD}{h}}{\frac{OB\cdot OC\sin\angle BOC}{h}\cdot\frac{OA\cdot OD\sin\angle AOD}{h}}=
=\frac{\sin\angle AOC\cdot\sin\angle BOD}{\sin\angle BOC\cdot\sin\angle AOD},
а так как
\angle AOC=\angle A_{1}OC_{1},~\angle BOC=\angle B_{1}OC_{1},~\angle AOD=\angle A_{1}OD_{1},~\angle BOD=\angle B_{1}OD_{1},
то
\frac{A_{1}C_{1}}{C_{1}B_{1}}:\frac{A_{1}D_{1}}{D_{1}B_{1}}=\frac{AC}{CB}:\frac{AD}{DB}.
Что и требовалось доказать.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 189-190
Источник: Курант Р., Роббинс Г. Что такое математика?. — 2-е изд. — М.: Просвещение, 1976. — с. 204
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 22

