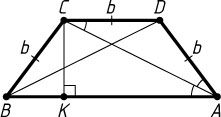
2030. В трапеции ABCD
основание AB
равно a
, основание CD
равно b
. Найдите площадь трапеции, если известно, что диагонали трапеции являются биссектрисами углов DAB
и ABC
.
Ответ. \frac{1}{4}(a+b)\sqrt{3b^{2}+2ab-a^{2}}
.
Указание. Треугольники ADC
и BDC
— равнобедренные.
Решение. Поскольку
\angle DCA=\angle CAB=\angle DAC,
то треугольник ADC
— равнобедренный. Поэтому AD=DC=b
. Аналогично CB=CD=b
.
Пусть CK
— высота треугольника ACB
. Тогда
CK=\sqrt{BC^{2}-KB^{2}}=\sqrt{b^{2}-\frac{(a-b)^{2}}{4}}=\frac{1}{2}\sqrt{3b^{2}+2ab-a^{2}}.
Следовательно, площадь трапеции равна
\frac{a+b}{2}\cdot CK=\frac{1}{4}(a+b)\sqrt{3b^{2}+2ab-a^{2}}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 42, с. 10
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 42, с. 8
