2032. Найдите площадь трапеции с основаниями 18 и 13 и боковыми сторонами 3 и 4.
Ответ. 37,2.
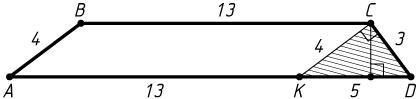
Указание. Через вершину меньшего основания трапеции проведите прямую, параллельную боковой стороне.
Решение. Через вершину C
меньшего основания BC
трапеции ABCD
(BC=13
, AD=18
, AB=4
, CD=3
) проведём прямую, параллельную боковой стороне AB
, до пересечения с основанием AD
в точке K
. Тогда
CK=AB=4,~DK=AD-AK=AD-BC=18-13=5,~CD=3.
Поскольку KD^{2}=CD^{2}+CK^{2}
, то треугольник KCD
— прямоугольный. Его высота, опущенная на гипотенузу, равна \frac{3\cdot4}{5}=\frac{12}{5}
. Следовательно,
S_{ABCD}=\frac{18+13}{2}\cdot\frac{12}{5}=37{,}2.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4, с. 5
