2033. Найдите площадь трапеции с основаниями 11 и 4 и диагоналями 9 и 12.
Ответ. 54.
Указание. Через вершину трапеции проведите прямую, параллельную диагонали.
Решение. Через вершину C
меньшего основания BC
трапеции ABCD
(BC=4
, AD=11
, AC=9
, BD=12
) проведём прямую, параллельную диагонали BD
, до пересечения с прямой AD
в точке K
. В треугольнике ACK
AC=9,~CK=BD=12,~AK=AD+DK=AD+BC=11+4=15.
Поскольку AK^{2}=AC^{2}+CK^{2}
, то треугольник ACK
— прямоугольный. Его площадь равна половине произведения катетов, т. е.
S_{\triangle ACK}=\frac{1}{2}AC\cdot CK=54.
Площадь трапеции ABCD
равна площади этого треугольника, так как равновелики треугольники ABC
и CDK
(BC=DK
, а высоты, опущенные на эти стороны, равны высоте трапеции).
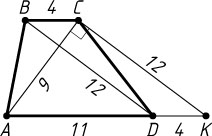
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.2, с. 30
