2034. Найдите площадь трапеции, параллельные стороны которой равны 16 и 44, а непараллельные — 17 и 25.
Ответ. 450.
Указание. Через вершину трапеции проведите прямую, параллельную боковой стороне.
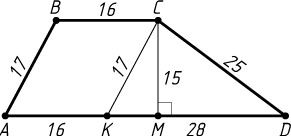
Решение. Через вершину C
трапеции ABCD
(BC=16
, AD=44
, AB=17
, CD=25
) проведём прямую, параллельную стороне AB
, до пересечения с основанием AD
в точке K
.
В треугольнике CKD
CK=17,~CD=25,~KD=AD-BC=28.
По формуле Герона
S_{\triangle CKD}=\sqrt{35\cdot7\cdot10\cdot18}=5\cdot7\cdot6=210.
Если CM
— высота этого треугольника, то
CM=\frac{2S_{\triangle CKD}}{KD}=\frac{2\cdot210}{28}=15.
Следовательно,
S_{ABCD}=\frac{AD+BC}{2}\cdot CM=450.
Примечание. Другие способы нахождения высоты CM
треугольника CKD
.
а) Обозначим DM=x
и найдём x
из уравнения
CD^{2}-DM^{2}=CK^{2}-KM^{2},~\mbox{или}~25^{2}-x^{2}=17^{2}-(28-x)^{2}.
Затем найдём CM
по теореме Пифагора из треугольника CMD
.
б) Найдём косинус угла CDK
по теореме косинусов из треугольника CDK
. Затем вычислим его синус и найдём CM
из прямоугольного треугольника CMD
Источник: Вступительный экзамен в МИУ. — 1980, № 50
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.184, с. 170
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.1, с. 30
