2036. Найдите площадь трапеции, диагонали которой равны 7 и 8, а основания — 3 и 6.
Ответ. 12\sqrt{5}
.
Указание. Через вершину трапеции проведите прямую, параллельную диагонали.
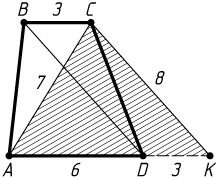
Решение. Через вершину C
меньшего основания BC
трапеции ABCD
(BC=3
, AD=6
, BD=8
, AC=7
) проведём прямую, параллельную диагонали BD
, до пересечения с прямой AD
в точке K
. Стороны треугольника ACK
равны:
AC=7,~CK=BD=8,~AK=AD+DK=AD+BC=6+3=9.
По формуле Герона
S_{\triangle ABC}=\sqrt{12\cdot5\cdot4\cdot3}=6\cdot2\sqrt{5}=12\sqrt{5}.
Следовательно,
S_{ABCD}=S_{\triangle ACK}=12\sqrt{5}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.288, с. 178
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 26
