2039. Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.
Ответ. 6.
Указание. Через вершину меньшего основания трапеции проведите прямую, параллельную диагонали.
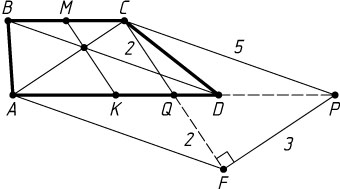
Решение. Пусть M
и K
— середины оснований BC
и AD
трапеции ABCD
. Через вершину C
меньшего основания BC
(AC=3
, BD=5
) проведём прямую, параллельную диагонали BD
, до пересечения с прямой AD
в точке P
и прямую, параллельную MK
, до пересечения с прямой AD
в точке Q
. Тогда
AQ=AK+KQ=AK+MC=\frac{1}{2}AD+\frac{1}{2}BC=
=\frac{1}{2}(AD+BC)=\frac{1}{2}(AD+DP).
Поэтому CQ
— медиана треугольника ACP
,
CQ=MK=2,~AC=3,~CP=BD=5,~S_{ABCD}=S_{\triangle ACP}.
На продолжении медианы CQ
за точку Q
отложим отрезок QF
, равный CQ
. Стороны треугольника CFP
равны:
CF=2CQ=4,~CP=BD=5,~FP=AC=3.
Этот треугольник прямоугольный (CP^{2}=CF^{2}+PF^{2}
). Поэтому
S_{\triangle CFP}=\frac{1}{2}CF\cdot PF=6.
Следовательно,
S_{ABCD}=S_{\triangle ACP}=S_{\triangle CFP}=6.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1973, вариант 1, № 2
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 268
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 169, с. 21
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 169, с. 20
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 16
