2043. Отношение оснований трапеции равно 3:2
, а отношение боковых сторон равно 5:3
. Точка пересечения биссектрис углов при большем основании трапеции лежит на меньшем основании. Найдите углы трапеции.
Ответ. 90^{\circ}
, 90^{\circ}
, \arcsin\frac{3}{5}
, 180^{\circ}-\arcsin\frac{3}{5}
.
Указание. Найдите отношение всех четырёх сторон трапеции. Затем через вершину меньшего основания проведите прямую, параллельную боковой стороне трапеции.
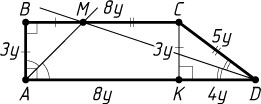
Решение. Пусть BC=2x
, AD=3x
— основания трапеции ABCD
, а AB=3y
, CD=5y
— её боковые стороны. Если M
— точка пересечения биссектрис углов A
и D
, то
BM=AB=3y,~CM=CD=5y.
Поэтому 5y+3y=2x
. Отсюда находим, что x=4y
. Следовательно, BC=8y
, AD=12y
.
Через точку C
проведём прямую, параллельную боковой стороне AB
, до пересечения с основанием AD
в точке K
. Стороны треугольника CKD
равны:
CK=AB=3y,~CD=5y,~KD=AD-AK=
=AD-BC=12y-8y=4y.
Поэтому треугольник CKD
— прямоугольный. Следовательно,
\angle CDK=\arcsin\frac{CK}{CD}=\arcsin\frac{3}{5},~\angle BAD=\angle CKD=90^{\circ}.
Источник: Вступительный экзамен в МФТИ. — 1980, билет 12, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 80-12-3, с. 229
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 6.29, с. 58
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.30.1, с. 61
