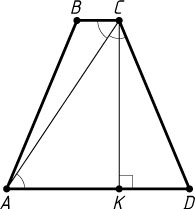
2046. Диагональ равнобедренной трапеции делит её тупой угол пополам. Меньшее основание трапеции равно 3, периметр равен 42. Найдите площадь трапеции.
Ответ. 96.
Указание. Докажите, что большее основание трапеции равно боковым сторонам.
Решение. Пусть BC
и AD
— основания трапеции ABCD
, BC=3
, CA
— биссектриса угла BCD
. Поскольку
\angle CAD=\angle BCA=\angle DCA,
то треугольник ACD
— равнобедренный. Поэтому
AD=CD=AB=\frac{42-3}{3}=13.
Из вершины C
опустим перпендикуляр CK
на основание AD
. Тогда
DK=\frac{AD-BC}{2}=\frac{13-3}{2}=5,
CK=\sqrt{CD^{2}-KD^{2}}=\sqrt{13^{2}-5^{2}}=12.
Следовательно,
S_{ABCD}=\frac{1}{2}(AD+BC)CK=96.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.102, с. 165
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 5, задача 2
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2, с. 168
