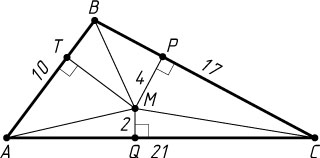
2048. Расстояния от точки M
, лежащей внутри треугольника ABC
, до его сторон AC
и BC
соответственно равны 2 и 4. Найдите расстояние от точки M
до прямой AB
, если AB=10
, BC=17
, AC=21
.
Ответ. \frac{29}{5}
.
Указание. Соедините данную точку M
с вершинами треугольника ABC
и рассмотрите площади трёх образовавшихся треугольников.
Решение. По формуле Герона
S_{\triangle ABC}=\sqrt{24\cdot3\cdot7\cdot14}=7\cdot3\cdot4=84.
Пусть P
и Q
— проекции точки M
на стороны BC
и AC
, а T
— на сторону AB
. Тогда
S_{\triangle ABC}=S_{\triangle BMC}+S_{\triangle AMC}+S_{\triangle AMB}=
=\frac{1}{2}BC\cdot MP+\frac{1}{2}AC\cdot MQ+\frac{1}{2}AB\cdot MT=
=\frac{1}{2}\cdot17\cdot4+\frac{1}{2}\cdot21\cdot2+\frac{1}{2}\cdot10\cdot MT=34+21+5MT.
Отсюда находим, что
MT=\frac{S_{\triangle ABC}-34-21}{5}=\frac{84-34-21}{5}=\frac{29}{5}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.258, с. 176
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.10, с. 39
