2049. Найдите площадь треугольника, если две его стороны равны 35 и 14, а биссектриса угла между ними равна 12.
Ответ. 235,2.
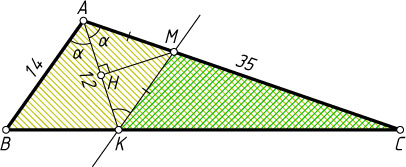
Указание. Пусть AK
— данная биссектриса треугольника ABC
. Найдите \sin\angle A
из уравнения S_{\triangle ABC}=S_{\triangle ACK}+S_{\triangle ABK}
.
Решение. Первый способ. Пусть AK
— биссектриса треугольника ABC
, в котором AC=35
, AB=14
, AK=12
. Обозначим \angle CAB=2\alpha
. Поскольку
S_{\triangle ABC}=S_{\triangle ACK}+S_{\triangle ABK},
то
\frac{1}{2}AC\cdot AB\sin2\alpha=\frac{1}{2}AC\cdot AK\sin\alpha+\frac{1}{2}AB\cdot AK\sin\alpha.
Применив формулу \sin2\alpha=2\sin\alpha\cos\alpha
, найдём из полученного уравнения, что \cos\alpha=\frac{3}{5}
. Тогда
\sin\alpha=\frac{4}{5},~\sin2\alpha=\frac{24}{25}.
Поэтому
S_{\triangle ABC}=\frac{1}{2}AC\cdot AB\cdot\sin2\alpha=\frac{1}{2}\cdot35\cdot14\cdot\frac{24}{25}=235{,}2.
Второй способ. По свойству биссектрисы треугольника
\frac{CK}{BK}=\frac{AC}{AB}=\frac{35}{14}=\frac{5}{2}.
Через точку K
проведём прямую, параллельную стороне AB
. Пусть эта прямая пересекает сторону AC
в точке M
. Тогда
\angle AKM=\angle KAB=\angle KAC,
поэтому треугольник AMK
— равнобедренный. Из подобия треугольников MKC
и ABC
находим, что
\frac{MK}{AB}=\frac{CK}{CB}=\frac{5}{7}.
Значит,
AM=MK=\frac{5}{7}AB=\frac{5}{7}\cdot14=10.
Высота MH
равнобедренного треугольника AMK
равна \sqrt{10^{2}-6^{2}}=8
. Поэтому
S_{\triangle AMK}=\frac{1}{2}\cdot12\cdot8=48.
Кроме того, \frac{BC}{CK}=\frac{7}{5}
, а по теореме о пропорциональных отрезках \frac{AC}{AM}=\frac{BC}{BK}=\frac{7}{2}
. Следовательно,
S_{\triangle ABC}=\frac{BC}{CK}\cdot S_{\triangle AKC}=\frac{BC}{CK}\cdot\frac{AC}{AM}\cdot S_{\triangle AMK}=\frac{7}{5}\cdot\frac{7}{2}\cdot48=235{,}2.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.343, с. 181
