2057. В трапеции ABCD
углы A
и D
при основании AD
соответственно равны 60^{\circ}
и 90^{\circ}
. Точка N
лежит на основании BC
, причём BN:BC=2:3
. Точка M
лежит на основании AD
, прямая MN
параллельна боковой стороне AB
и делит площадь трапеции пополам. Найдите AB:BC
.
Ответ. 4:3
.
Указание. Обозначьте NC=a
и выразите через a
высоту трапеции.
Решение. Обозначим NC=a
, AB=x
. Тогда BN=2a
, AM=BN=2a
. Если NK
— высота трапеции, то
DK=NC=a,~MK=\frac{1}{2}MN=\frac{1}{2}AB=\frac{x}{2}.
Из равенства площадей параллелограмма ABNM
и трапеции MNCD
следует равенство
2AM=NC+MD,~\mbox{или}~4a=a+a+\frac{x}{2}.
Отсюда находим, что x=4a
. Следовательно,
\frac{AB}{BC}=\frac{x}{3a}=\frac{4a}{3a}=\frac{4}{3}.
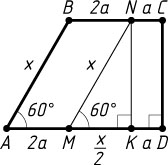
Источник: Вступительный экзамен на химический факультет МГУ. — 1972, вариант 2, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 162
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.12, с. 30
