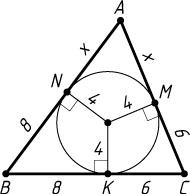
2063. В треугольник вписана окружность радиуса 4. Одна из сторон треугольника разделена точкой касания на части, равные 6 и 8. Найдите две другие стороны треугольника.
Ответ. 13 и 15.
Указание. Выразите площадь данного треугольника по формуле S=pr
и по формуле Герона.
Решение. Пусть K
, M
, N
— точки касания вписанной окружности со сторонами соответственно BC
, AC
и AB
треугольника ABC
; BK=8
, KC=6
. Тогда CM=KC=6
, BN=BK=8
.
Обозначим AM=AN=x
. Поскольку площадь треугольника равна произведению полупериметра треугольника на радиус вписанной окружности, то
S_{\triangle ABC}=(8+6+x)4=(14+x)4.
С другой стороны, по формуле Герона
S_{\triangle ABC}=\sqrt{(14+x)\cdot6\cdot8\cdot x}.
Решив уравнение
4(14+x)=\sqrt{(14+x)\cdot6\cdot8\cdot x},
найдём, что x=7
. Следовательно,
AC=x+6=13,~AB=x+8=15.
Источник: Вступительный экзамен в МАИ. — 1978
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.25, с. 88
