2068. В треугольнике ABC
известно, что BD
— медиана, BD=AB\cdot\frac{\sqrt{3}}{4}
, а \angle DBC=90^{\circ}
. Найдите угол ABD
.
Ответ. 30^{\circ}
.
Указание. Отложите на продолжении медианы BD
за точку D
отрезок, равный медиане.
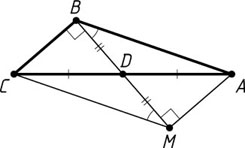
Решение. Пусть M
— точка на продолжении медианы BD
за точку D
, причём BD=DM
. Тогда ABCM
— параллелограмм,
MC=AB,~BM=2BD=AB\cdot\frac{\sqrt{3}}{2}.
Из прямоугольного треугольника MBC
находим, что
\cos\angle BMC=\frac{BM}{MC}=\frac{\sqrt{3}}{2}\cdot\frac{AB}{AB}=\frac{\sqrt{3}}{2}.
Следовательно,
\angle BMC=30^{\circ},~\angle ABD=\angle BMC=30^{\circ}.
