2079. В прямоугольном треугольнике ABC
биссектриса AP
острого угла A
делится центром O
вписанной окружности в отношении AO:OP=(\sqrt{3}+1):(\sqrt{3}-1)
. Найдите острые углы треугольника.
Ответ. 30^{\circ}
, 60^{\circ}
.
Указание. Примените свойство биссектрисы треугольника и найдите отношение большего катета к гипотенузе.
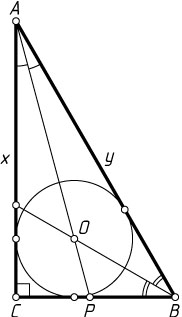
Решение. Обозначим: катет AC=x
, гипотенуза AB=y
. Пусть AP
— биссектриса треугольника ABC
.
По свойству биссектрисы треугольника
\frac{AC}{CP}=\frac{AO}{OP}=\frac{\sqrt{3}+1}{\sqrt{3}-1}.
Поэтому
CP=\frac{(\sqrt{3}-1)AC}{\sqrt{3}+1}=(2-\sqrt{3})x.
Аналогично
BP=\frac{\sqrt{3}-1)y}{\sqrt{3}+1}=(2-\sqrt{3})y.
По теореме Пифагора
x^{2}+(2-\sqrt{3})^{2}(x+y)^{2}=y^{2},
или
(7-4\sqrt{3})(x+y)^{2}=y^{2}-x^{2},
или
(7-4\sqrt{3})(x+y)=y-x.
Отсюда находим, что
(8-4\sqrt{3})x=(4\sqrt{3}-6)y.
Следовательно,
\cos\angle A=\frac{x}{y}=\frac{4\sqrt{3}-6}{8-4\sqrt{3}}=\frac{2\sqrt{3}(2-\sqrt{3})}{4(2-\sqrt{3})}=\frac{\sqrt{3}}{2}.
Поэтому \angle A=30^{\circ}
.
