2089. Медиана AD
остроугольного треугольника ABC
равна 5. Ортогональные проекции этой медианы на стороны AB
и AC
равны 4 и 2\sqrt{5}
соответственно. Найдите сторону BC
.
Ответ. 2\sqrt{10}
.
Указание. Найдите синусы и косинусы углов, образованных медианой со сторонами AB
и AC
, и воспользуйтесь равенством расстояний от вершин B
и C
до прямой AD
.
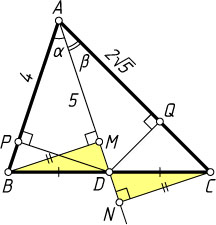
Решение. Пусть P
и Q
— проекции точки D
на AB
и AC
, M
и N
— проекции точек B
и C
на прямую AD
. Обозначим
\angle BAD=\alpha,~\angle CAD=\beta,~AB=a,~AC=b.
Тогда
\cos\alpha=\frac{AP}{AD}=\frac{4}{5},~\sin\alpha=\frac{3}{5},
\cos\beta=\frac{AQ}{AD}=\frac{2}{\sqrt{5}},~\sin\beta=\frac{1}{\sqrt{5}},
BM=AB\sin\alpha=\frac{3a}{5},~CN=AC\sin\beta=\frac{b}{\sqrt{5}}.
Из равенства прямоугольных треугольников CND
и BMD
следует, что BM=CN
, т. е. \frac{3a}{5}=\frac{b}{\sqrt{5}}
. Отсюда находим, что b=\frac{3a}{\sqrt{5}}
.
Выразив равные отрезки BD
и CD
по теореме косинусов из треугольников BAD
и CAD
соответственно, получим уравнение
a^{2}+25-2a\cdot5\cdot\frac{4}{5}=b^{2}+25-2b\cdot5\cdot\frac{2}{\sqrt{5}}.
Заменив b
на \frac{3a}{\sqrt{5}}
, получим, что a=5
.
По теореме косинусов из треугольника BAD
найдём, что BD=\sqrt{10}
. Следовательно, BC=2\sqrt{10}
.
Источник: Вступительный экзамен в МФТИ. — 1985, билет 5, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 85-5-4, с. 267
