2101. Диагонали BD
и AC
выпуклого четырёхугольника ABCD
перпендикулярны, пересекаются в точке O
, AO=2
, OC=3
. Точка K
лежит на стороне BC
, причём BK:KC=1:2
. Треугольник AKD
равносторонний. Найдите его площадь.
Ответ. \frac{7}{\sqrt{3}}
.
Указание. Докажите, что диагональ BD
делит отрезок AK
в отношении 2:1
.
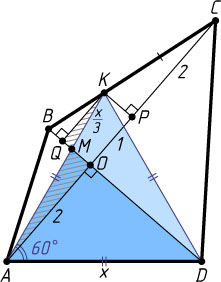
Решение. Пусть P
и Q
— проекции точки K
на диагонали AC
и BD
соответственно. Тогда
KQ=OP=\frac{1}{3}OC=1.
Если M
— точка пересечения отрезков AK
и QO
, то из подобия треугольников QMK
и OMA
следует, что
\frac{KM}{MA}=\frac{KQ}{AO}=\frac{1}{2}.
Обозначим AK=KD=AD=x
. Тогда MK=\frac{x}{3}
. По теореме косинусов из треугольника MKD
находим, что
DM^{2}=MK^{2}+KD^{2}-2MK\cdot KD\cos60^{\circ}=\frac{7x^{2}}{9},
откуда DM=\frac{x\sqrt{7}}{3}
. Поскольку AM=\frac{2}{3}AK
, то S_{\triangle AMD}=\frac{2}{3}S_{\triangle AKD}
, или
\frac{1}{2}x\cdot\frac{\sqrt{7}}{3}\cdot2=\frac{2}{3}\cdot\frac{1}{2}\cdot x^{2}\cdot\frac{\sqrt{3}}{2}.
Отсюда находим, что x=\frac{2\sqrt{7}}{\sqrt{3}}
. Следовательно,
S_{\triangle ABC}=\frac{x^{2}\sqrt{3}}{4}=\frac{7}{\sqrt{3}}.
Источник: Вступительный экзамен в МФТИ. — 1988, билет 1, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 88-1-3, с. 287
