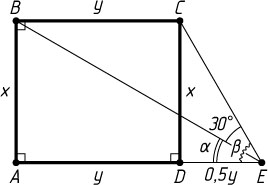
2110. На продолжении стороны AD
прямоугольника ABCD
за точку D
взята точка E
, причём DE=0{,}5AD
и \angle BEC=30^{\circ}
. Найдите отношение сторон прямоугольника ABCD
.
Ответ. \frac{\sqrt{3}}{2}
.
Указание. Примените формулу \tg(\beta-\alpha)=\frac{\tg\beta-\tg\alpha}{1+\tg\alpha\tg\beta}
.
Решение. Обозначим
\angle BEA=\alpha,~\angle CEA=\beta,~AB=CD=x,~BC=AD=y.
Тогда
\tg\alpha=\frac{AB}{AE}=\frac{2x}{3y},~\tg\beta=\frac{CD}{DE}=\frac{2x}{y},
\tg30^{\circ}=\tg(\beta-\alpha)=\frac{\tg\beta-\tg\alpha}{1+\tg\alpha\tg\beta}.
Подставим в правую часть этого равенства найденные выражения для \tg\alpha
и \tg\beta
через x
и y
. После упрощения получим уравнение
4x^{2}\sqrt{3}-12xy+3\sqrt{3}y^{2}=0,~\mbox{или}~4\sqrt{3}\left(\frac{x}{y}\right)^{2}-12\left(\frac{x}{y}\right)+3\sqrt{3}=0.
Отсюда находим, что \frac{x}{y}=\frac{\sqrt{3}}{2}
.
Источник: Вступительный экзамен в МФТИ. — 1981, билет 6, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 81-6-3, с. 234
