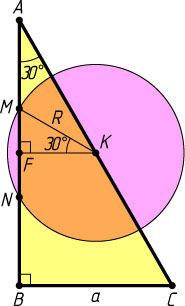
2113. Площадь треугольника ABC
равна 1, AC=2BC
, точка K
— середина стороны AC
. Окружность с центром в точке K
пересекает сторону AB
в точках M
и N
, при этом AM=MN=NB
. Найдите площадь части треугольника ABC
, заключённой внутри круга.
Ответ. \frac{2\pi\sqrt{3}}{27}+\frac{1}{6}
.
Указание. Докажите, что треугольник ABC
— прямоугольный.
Решение. Обозначим BC=a
, R
— радиус окружности. Тогда AC=2a
. Пусть F
— проекция центра K
окружности на сторону AB
. Тогда F
— середина MN
, а значит, и середина AB
. Поэтому KF
— средняя линия треугольника ABC
. Следовательно, треугольник ABC
— прямоугольный (\angle B=90^{\circ}
).
Поскольку AC=2BC
, то
\angle A=30^{\circ},~AB=a\sqrt{3},~MN=\frac{a\sqrt{3}}{3},~FM=\frac{1}{2}MN=\frac{a\sqrt{3}}{6},
KF=\frac{1}{2}BC=\frac{a}{2},~\angle FKM=30^{\circ},~R=KM=2FM=\frac{a\sqrt{3}}{3},
S_{\triangle NKM}=\frac{R^{2}\sqrt{3}}{4}=\frac{a^{2}\sqrt{3}}{12}.
Поскольку R\lt CK
(\frac{a\sqrt{3}}{3}\lt a
), то диаметр полукруга расположен внутри отрезка AC
. Кроме того, расстояние от точки K
до катета BC
больше, чем радиус полукруга (\frac{a\sqrt{3}}{2}\gt\frac{a\sqrt{3}}{3}
). Следовательно, искомая площадь равна разности площадей полукруга и сегмента, отсекаемого от полукруга хордой MN
, т. е.
\frac{\pi R^{2}}{2}-\left(\frac{\pi R^{2}}{6}-\frac{R^{2}\sqrt{3}}{4}\right)=R^{2}\left(\frac{\pi}{3}+\frac{\sqrt{3}}{4}\right)=\frac{1}{3}a^{2}\left(\frac{\pi}{3}+\frac{\sqrt{3}}{4}\right).
Поскольку S_{\triangle ABC}=\frac{a^{2}\sqrt{3}}{2}=1
, то a^{2}=\frac{2}{\sqrt{3}}
. Следовательно, искомая площадь равна
\frac{1}{3}\cdot\frac{2}{\sqrt{3}}\left(\frac{\pi}{3}+\frac{\sqrt{3}}{4}\right)=\frac{2\pi\sqrt{3}}{27}+\frac{1}{6}.
Источник: Вступительный экзамен в МФТИ. — 1981, билет 9, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 81-9-3, с. 236
