2121. В ромбе ABCD
угол \angle ABC=60^{\circ}
. Окружность касается прямой AD
в точке A
, центр окружности лежит внутри ромба. Касательные к окружности, проведённые из точки C
, перпендикулярны. Найдите отношение периметра ромба к длине окружности.
Ответ. \frac{\sqrt{3}+\sqrt{7}}{\pi}
.
Указание. Примените теорему косинусов к треугольнику AOC
(где O
— центр окружности).
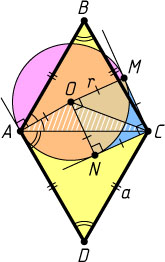
Решение. Пусть r
— радиус окружности, a
— сторона ромба, O
— центр окружности, M
и N
— точки касания окружности с касательными, проведёнными из вершины C
. Тогда AC=a
, CMON
— квадрат,
CO=r\sqrt{2},~OA=r,~\angle OAC=\angle OAD-\angle CAD=90^{\circ}-60^{\circ}=30^{\circ}.
По теореме косинусов из треугольника AOC
находим, что
OC^{2}=AO^{2}+AC^{2}-2AO\cdot AC\cos30^{\circ},
или
r^{2}+a^{2}-ar\sqrt{3}=2r^{2},~r^{2}+ar\sqrt{3}-a^{2}=0.
Отсюда находим, что
r=\frac{a(\sqrt{7}-\sqrt{3})}{2}.
Тогда искомое отношение равно
\frac{4a}{2\pi r}=\frac{\sqrt{3}+\sqrt{7}}{\pi}.
Источник: Вступительный экзамен в МФТИ. — 1982, билет 5, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 82-5-3, с. 243
