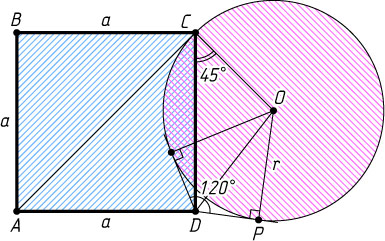
2123. Квадрат ABCD
и окружность расположены так, что окружность касается прямой AC
в точке C
, а центр окружности лежит по ту же сторону от прямой AC
, что и точка D
. Касательные к окружности, проведённые из точки D
образуют угол 120^{\circ}
. Найдите отношение площади квадрата к площади круга, ограниченного данной окружностью.
Ответ. \frac{4+\sqrt{15}}{3\pi}
.
Указание. С помощью теоремы косинусов выразите радиус окружности через сторону квадрата из треугольника DOC
, где O
— центр окружности.
Решение. Обозначим сторону квадрата через a
, радиус окружности — r
. Пусть O
— центр окружности, P
— точка касания окружности с одной из касательных, проведённых через точку D
. Из прямоугольного треугольника DPO
находим, что
DO=\frac{OP}{\sin\angle ODP}=\frac{2r}{\sqrt{3}}.
В треугольнике DOC
известно, что
DO=\frac{2r}{\sqrt{3}},~OC=r,~DC=a,~\angle DCO=45^{\circ}.
По теореме косинусов
DO^{2}=CO^{2}+CD^{2}-2CO\cdot CD\cos\angle DCO,~\mbox{или}~\frac{4r^{2}}{3}=r^{2}+a^{2}-ar\sqrt{2}.
Отсюда находим, что
r=\frac{a(\sqrt{30}-3\sqrt{2})}{2}.
Тогда искомое отношение равно
\frac{a^{2}}{\pi r^{2}}=\frac{4+\sqrt{15}}{3\pi}.
Источник: Вступительный экзамен в МФТИ. — 1982, билет 6, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 82-6-3, с. 243
