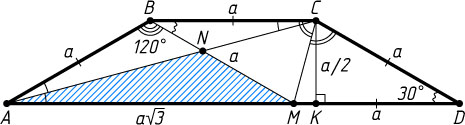
2129. В равнобедренной трапеции ABCD
углы при основании AD
равны 30^{\circ}
, диагональ AC
является биссектрисой угла BAD
. Биссектриса угла BCD
пересекает основание AD
в точке M
, а отрезок BM
пересекает диагональ AC
в точке N
. Найдите площадь треугольника ANM
, если площадь трапеции ABCD
равна 2+\sqrt{3}
.
Ответ. \frac{3(\sqrt{3}-1)}{2}
.
Указание. AN
— биссектриса равнобедренного треугольника ABM
.
Решение. Обозначим AB=CD=a
. Поскольку \angle BCA=\angle DAC=\angle BAC
, то треугольник ABC
— равнобедренный, BC=AB=a
. Аналогично докажем, что треугольник CDM
также равнобедренный, MD=CD=a
. Тогда BCDM
— ромб,
BM=CD=a,~\angle ABM=\angle ABC-\angle MBC=150^{\circ}-30^{\circ}=120^{\circ}.
Из равнобедренного треугольника ABM
(AB=BM=a
) находим, что AM=a\sqrt{3}
.
Поскольку AN
— биссектриса треугольника ABC
, то
\frac{MN}{NB}=\frac{AM}{AB}=\sqrt{3}.
Поэтому
\frac{MN}{BM}=\frac{\sqrt{3}}{\sqrt{3}+1}.
Следовательно,
S_{\triangle AMN}=\frac{\sqrt{3}}{\sqrt{3}+1}\cdot S_{\triangle ABM}=\frac{3a^{2}}{4(\sqrt{3}+1)}.
Пусть CK
— высота трапеции (CK=\frac{1}{2}CD=\frac{a}{2}
). Тогда
S_{ABCD}=\frac{1}{2}(AD+BC)\cdot CK,~\mbox{или}~2+\sqrt{3}=\frac{1}{4}(a\sqrt{3}+a+a)a=\frac{1}{4}a^{2}(2+\sqrt{3}).
Отсюда находим, что a^{2}=4.
Следовательно,
S_{\triangle AMN}=\frac{3a^{2}}{4(\sqrt{3}+1)}=\frac{3}{\sqrt{3}+1}=\frac{3(\sqrt{3}-1)}{2}.
Источник: Вступительный экзамен в МФТИ. — 1983, билет 1, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 83-1-3, с. 248
