2133. Окружность, построенная на стороне AD
параллелограмма ABCD
как на диаметре, проходит через середину диагонали AC
и пересекает сторону AB
в точке M
. Найдите отношение AM:AB
, если AC=3BD
.
Ответ. 4:5
.
Указание. Четырёхугольник ABCD
— ромб и \frac{AM}{AB}=\frac{AM}{AD}=\cos\angle BAD
.
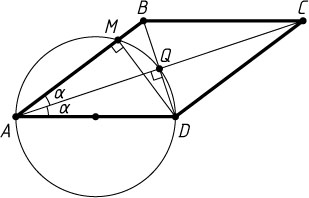
Решение. Пусть Q
— точка пересечения диагоналей AC
и BD
параллелограмма ABCD
. Вписанный угол AQD
опирается на диаметр AD
данной окружности. Поэтому \angle AQD=90^{\circ}
. Следовательно, ABCD
— ромб и AB=AD
.
Пусть \angle BAD=2\alpha
. Тогда
\angle QAD=\alpha,~\tg\alpha=\frac{DQ}{AQ}=\frac{BD}{AC}=\frac{1}{3},
\cos\angle BAD=\cos2\alpha=\frac{1-\tg^{2}\alpha}{1+\tg^{2}\alpha}=\frac{1-\frac{1}{9}}{1+\frac{1}{9}}=\frac{4}{5}.
Следовательно,
\frac{AM}{AB}=\frac{AM}{AD}=\cos2\alpha=\frac{4}{5}.
Источник: Вступительный экзамен в МФТИ. — 1983, билет 5, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 83-5-3, с. 251
