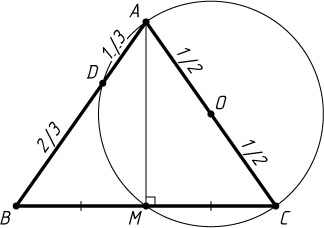
2145. Окружность, построенная на стороне AC
треугольника ABC
как на диаметре, проходит через середину стороны BC
и пересекает сторону AB
в точке D
так, что AD=\frac{1}{3}AB
. Найдите площадь треугольника ABC
, если AC=1
.
Ответ. \frac{\sqrt{2}}{3}
.
Указание. Треугольник ABC
— равнобедренный.
Решение. Пусть M
— середина BC
. Диаметр AC
виден из точки M
под прямым углом, значит, AM
— высота и медиана треугольника ABC
. Поэтому этот треугольник — равнобедренный, AB=AC=1
. Тогда
AD=\frac{1}{3},~BD=\frac{2}{3},
а так как BC\cdot BM=BA\cdot BD
, то 2BM^{2}=\frac{2}{3}
, BM=\frac{1}{\sqrt{3}}
. Поэтому
AM=\sqrt{AB^{2}-BM^{2}}=\sqrt{\frac{2}{3}}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AM=\frac{\sqrt{2}}{3}.
