2166. Найдите высоту равнобедренной трапеции, если её диагонали взаимно перпендикулярны, а площадь трапеции равна S
.
Ответ. \sqrt{S}
.
Указание. Через одну из вершин меньшего основания трапеции проведите прямую, параллельную диагонали, до пересечения с продолжением большего основания.
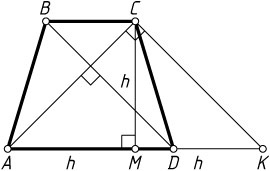
Решение. Через вершину C
меньшего основания BC
трапеции ABCD
проведём прямую, параллельную диагонали BD
, до пересечения с прямой AD
в точке K
. Получим равнобедренный прямоугольный треугольник ACK
(\angle C=90^{\circ})
, площадь которого равна площади данной трапеции, т. е. S
.
Пусть CM=h
— высота этого треугольника. Тогда CM
— высота трапеции и AM=MK=CM=h
. Следовательно,
S=\frac{1}{2}AK\cdot CM=h^{2}.
Отсюда находим, что h=\sqrt{S}
.
Источник: Вступительный экзамен в МФТИ. — 1970, № 2, билет 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 70-2-1, с. 139
