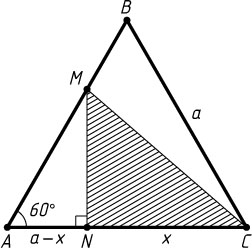
2216. В правильный треугольник ABC
вписан прямоугольный треугольник MNC
так, что вершина прямого угла N
лежит на AC
, а вершина M
лежит на стороне AB
. В каком отношении точка N
должна делить сторону AC
, чтобы площадь треугольника MNC
составляла \frac{4}{9}
площади треугольника ABC
?
Ответ. \frac{AN}{NC}=\frac{1}{2}
.
Решение. Пусть AB=AC=BC=a
, CN=x
. Из условия задачи следует, что x\gt\frac{a}{2}
.
Из прямоугольного треугольника ANM
находим, что
MN=AN\tg\angle MAN=(a-x)\tg60^{\circ}=(a-x)\sqrt{3}.
Тогда
S_{\triangle MNC}=\frac{1}{2}CN\cdot MN=\frac{1}{2}x\cdot(a-x)\sqrt{3}.
По условию
S_{\triangle MNC}=\frac{4}{9}S_{\triangle ABC},~\mbox{или}~\frac{x(a-x)\sqrt{3}}{2}=\frac{4}{9}\cdot\frac{a^{2}\sqrt{3}}{4}.
Из этого уравнения находим, что x=\frac{a}{3}
или x=\frac{2a}{3}
. Условию x\gt\frac{a}{2}
удовлетворяет только \frac{2}{3}a
. Следовательно,
\frac{AN}{NC}=\frac{a-x}{x}=\frac{\frac{a}{3}}{\frac{2a}{3}}=\frac{1}{2}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1974, № 3, вариант 3
