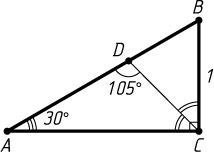
2227. В треугольнике ABC
проведена биссектриса CD
, при этом величины углов ADC
и CDB
относятся как 7:5
. Найдите AD
, если известно, что BC=1
, а угол BAC
равен 30^{\circ}
.
Ответ. 3-\sqrt{3}
.
Указание. Докажите, что треугольник ABC
прямоугольный и примените свойство биссектрисы треугольника.
Решение. Поскольку
\angle ADC=\frac{7}{12}\cdot180^{\circ}=105^{\circ},
то
\angle ACD=180^{\circ}-30^{\circ}-105^{\circ}=45^{\circ}.
Поэтому \angle ACB=90^{\circ}
, т. е. треугольник ABC
— прямоугольный. Тогда
AC=BC\tg\angle ABC=\sqrt{3},~AB=2BC=2.
По свойству биссектрисы треугольника
\frac{AD}{DB}=\frac{AC}{BC}=\sqrt{3}.
Значит,
\frac{AD}{AB}=\frac{\sqrt{3}}{\sqrt{3}+1}.
Следовательно,
AD=\frac{2\sqrt{3}}{\sqrt{3}+1}=\frac{2\sqrt{3}(\sqrt{3}-1)}{2}=\sqrt{3}(\sqrt{3}-1)=3-\sqrt{3}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1989, № 4, вариант 1
