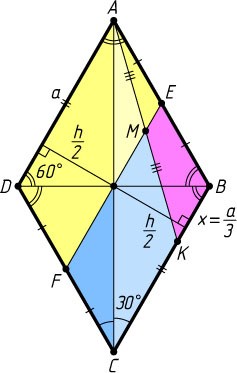
2230. В ромбе ABCD
со стороной a
угол при вершине A
равен 60^{\circ}
, точки E
и F
являются серединами сторон AB
и CD
соответственно. Точка K
лежит на стороне BC
, отрезки AK
и EF
пересекаются в точке M
. Найдите MK
, если известно, что площадь четырёхугольника MKCF
составляет \frac{3}{8}
площади ромба ABCD
.
Ответ. \frac{a\sqrt{13}}{6}
.
Указание. Из равенства S_{BKME}=\frac{1}{8}S_{ABCD}
выведите, что BK=\frac{a}{3}
.
Решение. Поскольку S_{MKCF}=\frac{3}{8}S_{ABCD}
, то
S_{BKME}=S_{BCFE}-S_{MKCF}=\frac{1}{2}S_{ABCD}-\frac{3}{8}S_{ABCD}=\frac{1}{8}S_{ABCD}.
Если h
— высота ромба, то площадь трапеции MKBE
равна \frac{BK+ME}{2}\cdot\frac{h}{2}
. Обозначив BK
через x
, получим уравнение
\frac{x+\frac{x}{2}}{2}\cdot\frac{h}{2}=\frac{ah}{8}.
Отсюда находим, что x=\frac{a}{3}
. Тогда
CK=BC-BK=a-\frac{a}{3}=\frac{2a}{3}.
По теореме косинусов из треугольника ACK
находим, что
AK^{2}=CA^{2}+CK^{2}-2CA\cdot CK\cos30^{\circ}=3a^{2}+\frac{4a^{2}}{9}-2a^{2}=\frac{13a^{2}}{9}.
Следовательно,
MK=\frac{1}{2}AK=\frac{a\sqrt{13}}{6}.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1974, вариант 2, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 92
