2239. Найдите площадь треугольника ABC
, если AC=3
, BC=4
, а медианы AK
и BL
взаимно перпендикулярны.
Ответ. \sqrt{11}
.
Указание. Медианы треугольника делятся точкой пересечения в отношении 2:1
, считая от вершины.
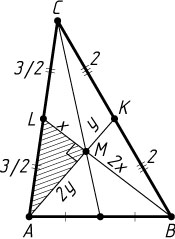
Решение. Пусть M
— точка пересечения медиан треугольника ABC
. Обозначим ML=x
, MK=y
. Тогда MB=2x
, MA=2y
. По теореме Пифагора из прямоугольных треугольников BMK
и AML
находим:
\syst{4x^{2}+y^{2}=4\\x^{2}+4y^{2}=\frac{9}{4}.\\}
Из полученной системы находим, что
x=\frac{\sqrt{11}}{2\sqrt{3}},~y=\frac{1}{\sqrt{3}}.
Поэтому
S_{\triangle AMB}=\frac{1}{2}AM\cdot MB=\frac{1}{2}\cdot2x\cdot2y=2xy=\frac{\sqrt{11}}{3}.
Следовательно,
S_{\triangle ABC}=3S_{\triangle AMB}=\sqrt{11}.
Источник: Вступительный экзамен на химический факультет МГУ. — 1970, № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 1.36, с. 14
