2244. В остроугольном треугольнике две высоты равны 3 и 2\sqrt{2}
, а их точка пересечения делит третью высоту в отношении 5:1
, считая от вершины треугольника. Найдите площадь треугольника.
Ответ. 6.
Указание. Пусть \alpha
и \beta
— острые углы треугольника, из вершин которых проведены данные высоты. Составьте систему тригонометрических уравнений относительно \alpha
и \beta
.
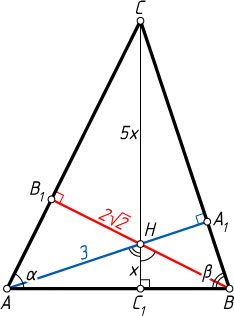
Решение. Пусть AA_{1}
, BB_{1}
и CC_{1}
— высоты треугольника ABC
, H
— точка их пересечения; AA_{1}=3
, BB_{1}=2\sqrt{2}
. Обозначим
\angle CAB=\alpha,~\angle ABC=\beta,~HC_{1}=x.
Тогда
CC_{1}=6x,~\angle AHC_{1}=\beta,~\angle BHC_{1}=\alpha.
Из прямоугольных треугольников AA_{1}B
и BB_{1}A
находим, что
AB=\frac{3}{\sin\beta}=\frac{2\sqrt{2}}{\sin\alpha}.
Поэтому \sin\beta=\frac{3\sin\alpha}{2\sqrt{2}}
. Из прямоугольных треугольников BC_{1}C
и BC_{1}H
находим, что
BC_{1}=\frac{6x}{\tg\beta}=x\tg\alpha.
Поэтому
\tg\alpha\tg\beta=6~\Rightarrow~\sin\alpha\sin\beta=6\cos\alpha\cos\beta~\Rightarrow~\sin^{2}\alpha\sin^{2}\beta=36\cos^{2}\alpha\cos^{2}\beta.
Подставим в последнее уравнение
\sin^{2}\beta=\frac{9\sin^{2}\alpha}{8},~\cos^{2}\beta=1-\sin^{2}\beta=1-\frac{9\sin^{2}\alpha}{8},~\cos^{2}\alpha=1-\sin^{2}\alpha.
Получим уравнение
35\sin^{4}\alpha-68\sin^{2}\alpha+32=0,
из которого находим, что \sin\alpha=\frac{2}{\sqrt{5}}
(\alpha
и \beta
меньше 90^{\circ}
). Поэтому
\cos\alpha=\frac{1}{\sqrt{5}},~\sin\beta=\frac{3}{\sqrt{10}},~\cos\beta=\frac{1}{\sqrt{10}},~AB=\frac{3}{\sin\beta}=\sqrt{10}.
Из треугольника ABC
находим по теореме синусов:
AC=\frac{AB\sin\beta}{\sin(\alpha+\beta)}=3\sqrt{2}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin\alpha=\frac{1}{2}\cdot\sqrt{10}\cdot3\sqrt{2}\cdot\frac{2}{\sqrt{5}}=6.
Источник: Вступительный экзамен в МФТИ. — 1966, билет 2, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 66-2-3, с. 115
