2250. Найдите площадь треугольника, если две стороны его соответственно равны 27 и 29, а медиана, проведённая к третьей, равна 26.
Ответ. 270.
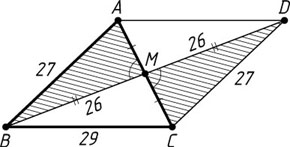
Указание. Достройте треугольник до параллелограмма и примените формулу Герона.
Решение. Пусть стороны AB
и BC
треугольника ABC
равны соответственно 27 и 29, а его медиана BM
равна 26. На продолжении медианы BM
за точку M
отложим отрезок MD
, равный BM
. Из равенства треугольников ABM
и CDM
(по двум сторонам и углу между ними) следует равенство площадей треугольников ABC
и BCD
. В треугольнике BCD
известно, что
BC=29,~BD=2BM=52,~DC=AB=27.
По формуле Герона
S_{\triangle BCD}=\sqrt{54(54-52)(54-29)(54-27)}=\sqrt{54\cdot2\cdot25\cdot27}=27\cdot2\cdot5=270.
Следовательно,
S_{\triangle ABC}=S_{\triangle BCD}=270.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 65, с. 83
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 2.3, с. 17
