2255. В прямоугольный треугольник вписан квадрат так, что одна из его сторон находится на гипотенузе. Боковые отрезки гипотенузы равны m
и n
. Найдите площадь квадрата.
Ответ. mn
.
Указание. Через вершину квадрата, принадлежащую катету данного треугольника, проведите прямую, параллельную другому катету.
Решение. Пусть вершины M
и N
квадрата MNKL
находятся соответственно на катетах AC
и BC
прямоугольного треугольника ABC
, а вершины K
и L
— на гипотенузе AB
. При этом AL=m
, BK=n
.
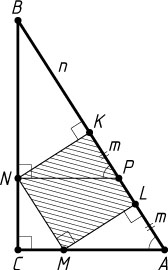
Первый способ. Через точку N
проведём прямую, параллельную AC
, до пересечения с гипотенузой AB
в точке P
. Из равенства прямоугольных треугольников AML
и PNK
следует, что PK=AL=m
.
Сторона NK
указанного квадрата есть высота прямоугольного треугольника PNB
, проведённая из вершины прямого угла. Поэтому
NK^{2}=PK\cdot BK=mn.
Следовательно, площадь квадрата MNLK
равна mn
.
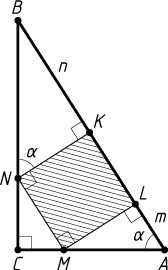
Второй способ. Обозначим \angle BAC=\alpha
. Тогда \angle BKN=\alpha
. Из прямоугольных треугольников ALM
и NKB
находим, что
\tg\alpha=\frac{ML}{AL},~\tg\alpha=\frac{BK}{KN},
поэтому
\frac{ML}{AL}=\frac{KB}{KN}.
Следовательно,
S_{MNKL}=ML^{2}=ML\cdot KN=AL\cdot BK=mn.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 39, с. 76
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 25, с. 79
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.3, с. 23

