2264. В сегмент, дуга которого равна 60^{\circ}
, вписан квадрат. Найдите площадь квадрата, если радиус круга равен 2\sqrt{3}+\sqrt{17}
.
Ответ. 1.
Указание. Обозначьте через x
сторону квадрата и примените теорему Пифагора к треугольнику с вершинами: в центре окружности, в середине стороны квадрата и в вершине квадрата, принадлежащей этой стороне.
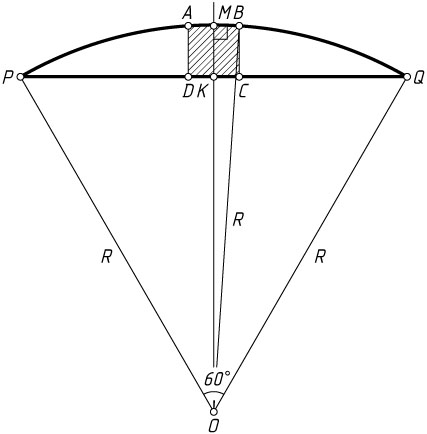
Решение. Пусть O
— центр окружности, R
— её радиус (R=2\sqrt{3}+\sqrt{17}
), x
— сторона квадрата ABCD
, причём точки C
и D
принадлежат хорде PQ
данного сегмента.
Проведём через центр окружности прямую, перпендикулярную PQ
. Пусть K
и M
— точки её пересечения с хордами PQ
и AB
. Тогда
OK=\frac{R\sqrt{3}}{2},~MB=\frac{x}{2},~KM=x.
Рассмотрим прямоугольный треугольник OMB
. По теореме Пифагора
(OK+KM)^{2}+MB^{2}=OB^{2},~\mbox{или}~\left(\frac{R\sqrt{3}}{2}+x\right)^{2}+\frac{x^{2}}{4}=R^{2}.
Отсюда находим, что
x=\frac{R(\sqrt{17}-2\sqrt{3})}{5}=\frac{(2\sqrt{3}+\sqrt{17})(\sqrt{17}-2\sqrt{3})}{5}=1.
Следовательно, S_{ABCD}=1
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.189, с. 171
