2269. Задача о «луночках» Гиппократа. На гипотенузе и катетах прямоугольного треугольника как на диаметрах построены полуокружности так, как показано на рисунке. Докажите, что сумма площадей заштрихованных «луночек» равна площади треугольника.
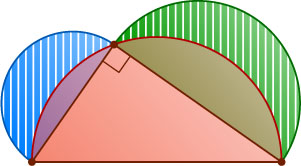
Указание. Сумма площадей указанных «луночек» получается вычитанием площади большого полукруга из суммы площадей двух меньших полукругов и площади треугольника.
Решение. Пусть a
и b
— катеты треугольника, c
— гипотенуза. Тогда сумма S
площадей указанных «луночек» получается вычитанием площади большого полукруга из суммы площадей двух меньших полукругов и площади треугольника. Следовательно,
S=\frac{\pi a^{2}}{8}+\frac{\pi b^{2}}{8}+\frac{1}{2}ab-\frac{\pi c^{2}}{8}=\frac{\pi}{8}(a^{2}+b^{2}-c^{2})+\frac{1}{2}ab=\frac{1}{2}ab,
что и требовалось доказать.
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 41, с. 34
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.38, с. 63
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.39, с. 61
