2272. Точки D
, E
и F
выбраны на сторонах AC
, AB
и BC
равнобедренного треугольника ABC
(AB=BC)
так, что DE=DF
и при этом \angle BAC=\angle FDE
. Докажите, что AE+FC=AC
.
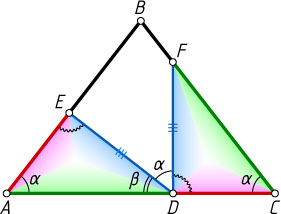
Решение. Обозначим \angle BAC=\angle ACB=\alpha
, \angle ADE=\beta
. Треугольники AED
и CDF
равны по стороне и двум прилежащим к ней углам, так как
DE=DF,~\angle DAE=\angle DCF,~\angle AED=180^{\circ}-\alpha-\beta=\angle CDF,
поэтому AE=CD
и AD=CF
. Следовательно, AE+FC=CD+AD=AC
. Что и требовалось доказать.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1993, отборочный тур, 10 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 93.50
