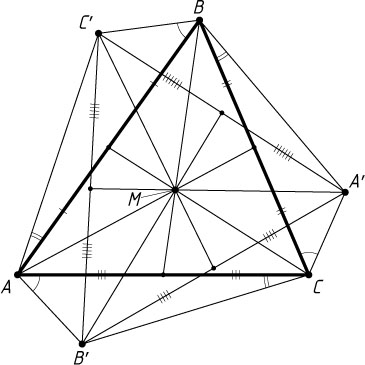
2283. На сторонах треугольника ABC
внешним образом построены подобные треугольники: \triangle A'BC\sim\triangle B'CA\sim\triangle C'AB
. Докажите, что в треугольниках ABC
и A'B'C'
точки пересечения медиан совпадают.
Решение. Пусть P
— поворотная гомотетия, переводящая вектор \overrightarrow{CB}
в вектор \overrightarrow{CA'}
, т. е. P(\overrightarrow{CB})=\overrightarrow{CA'}
. Из равенства соответствующих углов и пропорциональности соответствующих сторон подобных треугольников следует, что
P(\overrightarrow{BA})=\overrightarrow{BC'},~P(\overrightarrow{AC})=\overrightarrow{AB'},
поэтому
\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=(\overrightarrow{AC}+\overrightarrow{CA'})+(\overrightarrow{BA}+\overrightarrow{AB'})+(\overrightarrow{CB}+\overrightarrow{BC'})=
=\overrightarrow{AC}+P(\overrightarrow{CB})+\overrightarrow{BA}+P(\overrightarrow{AC})+\overrightarrow{CB}+P(\overrightarrow{BA})=
=(\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{BA})+(P(\overrightarrow{AC})+P(\overrightarrow{CB})+P(\overrightarrow{BA}))=\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}.
Пусть M
и M'
— точки пересечения медиан треугольников ABC
и A'B'C'
соответственно. Тогда
\overrightarrow{MM'}=\frac{1}{3}(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'})=\frac{1}{3}\cdot\overrightarrow{0}=\overrightarrow{0}.
Следовательно, точки M
и M'
совпадают.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 19.32, с. 88
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 19.33, с. 392
Источник: Математика в задачах: Сб. материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду / Под ред. А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова и др. — М.: МЦНМО, 2009. — № 5, с. 181
