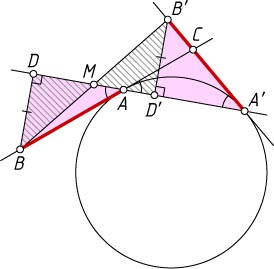
2289. Прямая касается окружности в точке A
. На прямой выбрали точку B
и повернули отрезок AB
на некоторый угол вокруг центра окружности, получив отрезок A'B'
. Докажите, что прямая, проходящая через точки касания A
и A'
, делит пополам отрезок BB'
.
Решение. Пусть прямые AA'
и BB'
пересекаются в точке M
. Если AA'
— диаметр, то утверждение очевидно. Предположим, что AA'
— не диаметр. Тогда прямые AB
и A'B'
пересекаются в некоторой точке C
.
Опустим перпендикуляры BD
и B'D'
из точек B
и B'
на прямую AA'
. Тогда
\angle BAD=\angle CAA'=\angle CA'A=\angle B'A'D',
значит, прямоугольные треугольники BAD
и B'A'D'
равны по гипотенузе и острому углу. Следовательно, BD=B'D'
. Тогда прямоугольные треугольники BDM
и B'D'M
равны по катету и противолежащему острому углу. Следовательно, BM=B'M
, т. е. M
— середина BB'
. Что и требовалось доказать.
Автор: Женодаров Р. Г.
Источник: Турнир городов. — 2006-2007, весенний тур, старшие классы, тренировочный вариант
