2298. Четырёхугольник ABCD
— вписанный, AB=AD
. На стороне BC
взята точка M
, а на стороне CD
— точка N
так, что угол MAN
равен половине угла BAD
. Докажите, что MN=BM+ND
.
Указание. Отразите стороны AB
и AD
относительно прямых AM
и AN
соответственно или рассмотрите поворот вокруг вершины A
, переводящий вершину B
в D
.
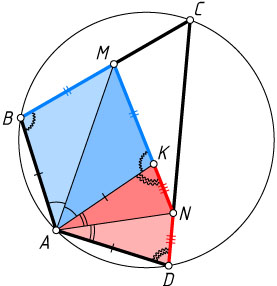
Решение. Первый способ. Отразим стороны AB
и AD
относительно прямых AM
и AN
соответственно (рис. 1). Поскольку \angle BAD=2\angle MAN
, лучи AB
и AD
перейдут в один и тот же луч, а так как AB=AD
, то точки B
и D
перейдут в одну и ту же точку K
.
Из равенства треугольников AKM
и ABM
следует, что \angle AKM=\angle ABM
и MK=BM
, а из равенства треугольников AKN
и ADN
— \angle AKN=\angle ADN
и NK=ND
. Четырёхугольник ABCD
— вписанный, поэтому
\angle AKM+\angle AKN=\angle ABM+\angle ADN=\angle ABC+\angle ADC=180^{\circ}.
Значит, точка K
лежит на отрезке MN
. Следовательно,
BM+ND=MK+NK=MN.
Что и требовалось доказать.
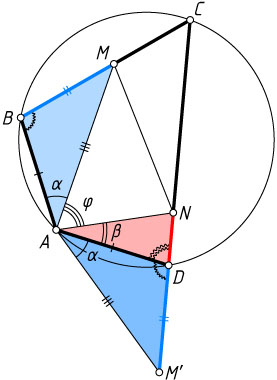
Второй способ. При повороте вокруг вершины A
, переводящем луч AB
в луч AD
(рис. 2), вершина B
переходит в D
, точка M
— в некоторую точку M'
, а треугольник ABM
— в равный ему треугольник ADM'
. Поскольку \angle ADM'=\angle ABM
, а четырёхугольник ABCD
— вписанный,
\angle ADM'+\angle ADN=\angle ABM+\angle ADN=\angle ABC+\angle ADC=180^{\circ}.
Значит, точка M'
лежит на прямой CD
.
Из равенства треугольников ADM'
и ABM
следует равенство углов DAM'
и BAM
, а также сторон M'D
и BM
. Обозначим
\angle DAM'=\angle BAM=\alpha,~\angle DAN=\beta,~\angle MAN=\varphi.
По условию задачи \varphi=\frac{\alpha+\beta+\varphi}{2}
, откуда \angle MAN=\varphi=\alpha+\beta=\angle NAM'
, значит, треугольники MAN
и AM'N
равны по двум сторонам и углу между ними. Следовательно,
MN=M'N=M'D+ND=BM+ND.
Что и требовалось доказать.
Автор: Малкин М. И.
Источник: Турнир городов. — 2005-2006, XXVII, весенний тур, старшие классы, основной вариант

