2299. Дан остроугольный треугольник ABC
. На сторонах AB
и BC
во внешнюю сторону построены равные прямоугольники ABMN
и LBCK
так, что LB=AB
. Докажите, что прямые AL
, CM
и NK
пересекаются в одной точке.
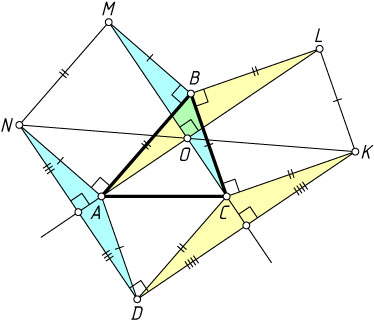
Решение. Первый способ. Достроим треугольник ABC
до параллелограмма ABCD
. Поскольку AD=BC=LK
и AD\parallel BC\parallel LK
, четырёхугольник ALKD
— параллелограмм. Аналогично четырёхугольник CDNM
— также параллелограмм. Значит, DK\parallel AL
и DN\parallel MC
.
Боковые стороны подобных равнобедренных треугольников CBM
и ABL
соответственно перпендикулярны, значит, перпендикулярны и их основания CM
и AL
. Поэтому параллельные им прямые DN
и DK
также перпендикулярны.
Прямая MC
перпендикулярна отрезку DK
и проходит через точку C
, равноудалённую от D
и K
(CD=AB=BL=CK
), поэтому прямая MC
— серединный перпендикуляр к отрезку DK
. Аналогично прямая LA
— серединный перпендикуляр к отрезку DN
. Серединные перпендикуляры к катетам DK
и DN
прямоугольного треугольника KDN
пересекаются в середине гипотенузы KN
. Следовательно, в этой точке пересекаются прямые AL
, CM
и NK
. Что и требовалось доказать.
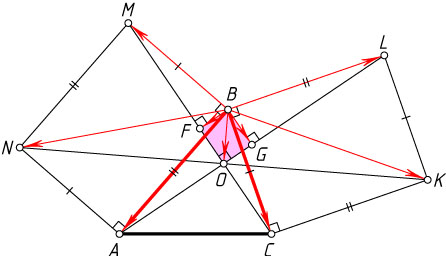
Второй способ. Пусть F
и G
— середины AL
и CM
соответственно, O
— точка пересечения прямых AL
и CM
. Боковые стороны подобных равнобедренных треугольников CBM
и ABL
соответственно перпендикулярны, значит, перпендикулярны и их основания CM
и AL
. Поэтому BFOG
— прямоугольник. Тогда
\overrightarrow{BO}=\overrightarrow{BF}+\overrightarrow{BG}=\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BL})+\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{BM})=
=\frac{1}{2}\left((\overrightarrow{BC}+\overrightarrow{BL})+(\overrightarrow{BA}+\overrightarrow{BM})\right)=\frac{1}{2}(\overrightarrow{BK}+\overrightarrow{BN}).
Из единственности разложения вектора по двум неколлинеарным векторам следует, что O
— середина отрезка KN
. Значит, прямые AL
, CM
и NK
пересекаются в точке O
. Что и требовалось доказать.
Примечание. В следующей формулировке задача предлагалась на Первых международных математических соревнованиях Саманйолу колледжа в Турции (см. Квант, 1997, N5, с.53).
На сторонах AB
и AC
остроугольного треугольника ABC
во внешнюю сторону построены прямоугольники ABB_{1}B_{2}
и ACC_{1}C_{2}
соответственно, причём AC_{2}=AB
и AB_{2}=AC
. Прямые BC_{2}
и B_{2}C
пересекаются в точке S
. Докажите, что:
а) угол BSC
— прямой;
б) точка S
лежит на прямой B_{1}C_{1}
.
Автор: Гаврилюк А. А.
Источник: Журнал «Квант». — 1997, № 5, с. 53, задача 5
Источник: Турнир городов. — 2005-2006, XXVII, весенний тур, младшие классы, основной вариант

