2301. Даны окружность и прямая, не пересекающая окружность. Как с помощью циркуля и линейки построить квадрат, две соседние вершины которого лежат на данной окружности, а две другие вершины — на данной прямой (если известно, что такой квадрат существует)?
Указание. Примените гомотетию.
Решение. Предположим, что нужный квадрат ABCD
построен, причём вершины C
и D
лежат на данной окружности с центром O
, а вершины C
и D
— на данной прямой. Опустим перпендикуляр OK
из центра окружности на её хорду CD
. Поскольку K
— середина CD
и OK\perp AB
, то прямая OK
проходит через середину M
отрезка AB
. При гомотетии с центром M
квадрат ABCD
перейдёт в в квадрат A_{1}B_{1}C_{1}D_{1}
, причём точка M
— середина стороны A_{1}B_{1}
этого квадрата.
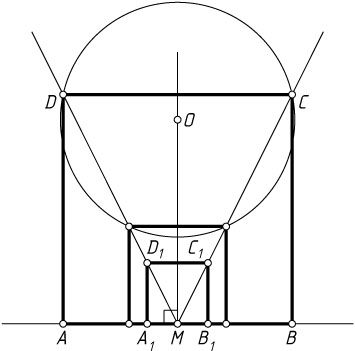
Отсюда вытекает следующее построение. Через центр O
данной окружности проведём прямую, перпендикулярную данной прямой. Пусть M
— точка пересечения проведённой прямой с данной. На данной прямой откладываем произвольные равные отрезки MA_{1}
и MB_{1}
так, чтобы точки A_{1}
и B_{1}
лежали по разные стороны от M
. Затем строим квадрат A_{1}B_{1}C_{1}D_{1}
. Если прямая MC_{1}
пересекает данную окружность, то каждая точка C
пересечения есть вершина искомого квадрата. Дальнейшее построение очевидно.
Автор: Кустарёв А. А.
Источник: Турнир городов. — 2004-2005, XXVI, осенний тур, младшие классы, тренировочный вариант
