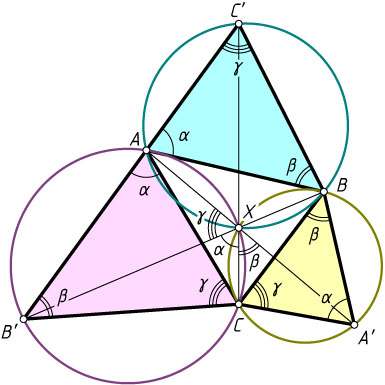
2302. Три окружности проходят через точку X
. Пусть A
, B
и C
— точки из пересечения, отличные от X
, A'
— вторая точка пересечения прямой AX
с описанной окружностью треугольника BCX
. Точки B'
и C'
определяются аналогично. Докажите, что треугольники ABC'
, AB'C
и A'BC
подобны.
Решение. Рассмотрим случай, изображённый на рисунке. Обозначим
\angle AXB'=\gamma,~\angle CXB'=\alpha,~\angle CXA'=\beta.
Тогда \alpha+\beta+\gamma=180^{\circ}
. Вписанные углы CXB'
и CAB'
опираются на одну и ту же дугу описанной окружности треугольника AB'C
, а вписанные углы BXC'
и BAC'
опираются на одну и ту же дугу описанной окружности треугольника ABC'
, поэтому
\angle BAC'=\angle BXC'=\angle CXB'=\angle CAB'=\alpha,
Аналогично
\angle ABC'=\angle AXC'=\angle CXA'=\angle CBA'=\beta,
\angle BCA'=\angle BXA'=\angle AXB'=\angle ACB'=\gamma.
Тогда
\angle BA'C=180^{\circ}-\beta-\gamma=\alpha,
\angle AB'C=180^{\circ}-\alpha-\gamma=\beta,
\angle AC'B=180^{\circ}-\alpha-\beta=\gamma.
Значит, соответствующие углы треугольников ABC'
, AB'C
и A'BC
равны. Следовательно, эти треугольники подобны.
Аналогично для остальных случаев.
Примечание. Можно обойтись без разбора случаев, если рассматривать ориентированные углы.
Автор: Заславский А. А.
Источник: Турнир городов. — 2004-2005, XXVI, осенний тур, старшие классы, тренировочный вариант
