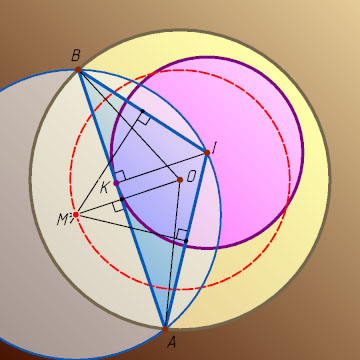
2305. Окружность с центром I
лежит внутри окружности с центром O
. Найдите геометрическое место центров описанных окружностей треугольников IAB
, где AB
— хорда большей окружности, касающаяся меньшей.
Ответ. Окружность с центром O
и радиусом \frac{R^{2}-d^{2}}{2r}
, где R\gt r
— радиусы данных окружностей, а d
— расстояние между их центрами.
Решение. Пусть R
и r
— радиусы большей и меньшей окружностей соответственно, d=OI
, K
— точка касания меньшей окружности с хордой AB
большей окружности, M
— центр описанной окружности треугольника AIB
.
Точки O
и M
лежат на серединном перпендикуляре к хорде AB
, поэтому OM\parallel IK
. Тогда
R^{2}-d^{2}=OA^{2}-OI^{2}=(\overrightarrow{OM}+\overrightarrow{MA})^{2}-(\overrightarrow{OM}+\overrightarrow{MI})^{2}=
=MA^{2}-MI^{2}+2\overrightarrow{OM}(\overrightarrow{MA}-\overrightarrow{MI})=MA^{2}-MI^{2}+2\overrightarrow{OM}\cdot\overrightarrow{IA}=
=MA^{2}-MI^{2}+2\overrightarrow{OM}(\overrightarrow{IK}+\overrightarrow{KA})=MA^{2}-MI^{2}+2\overrightarrow{OM}\cdot\overrightarrow{IK}
(\overrightarrow{OM}\cdot\overrightarrow{KA}=0
, так как OM\perp KA
).
Заметим, что доказанное равенство верно для любой точки M
, лежащей на серединном перпендикуляре к хорде AB
.
Поскольку MA=MI
как радиусы одной окружности,
R^{2}-d^{2}=2\overrightarrow{OM}\cdot\overrightarrow{IK}=\pm2r\cdot OM,
а так как R\gt d
, то R^{2}-d^{2}=2r\cdot OM
. Отсюда находим, что
OM=\frac{R^{2}-d^{2}}{2r}.
Следовательно, точка M
лежит на окружности S
радиуса \frac{R^{2}-d^{2}}{2r}
с центром O
.
Обратно, пусть M
— произвольная точка окружности S
. Проведём хорду AB
большей из данных окружностей, касающуюся меньшей в некоторой точке K
и перпендикулярную OM
. Таких хорд две. Возьмём ту из них, для которой вектор \overrightarrow{IK}
сонаправлен с вектором \overrightarrow{OM}
. Точка M
лежит на серединном перпендикуляре к отрезку AB
, поэтому MA=MB
. Кроме того OM=\frac{R^{2}-d^{2}}{2r}
и \overrightarrow{OM}\cdot\overrightarrow{IK}=r\cdot OM
, значит,
MA^{2}-MI^{2}=R^{2}-d^{2}-2\overrightarrow{OM}\cdot\overrightarrow{IK}=
=R^{2}-d^{2}-2r\cdot OM=R^{2}-d^{2}-2r\cdot\frac{R^{2}-d^{2}}{2r}=0.
Поэтому MA=MB=MI
. Следовательно, M
— центр описанной окружности треугольника IAB
.
Автор: Заславский А. А.
Источник: Турнир городов. — 2004-2005, XXVI, осенний тур, старшие классы, основной вариант
