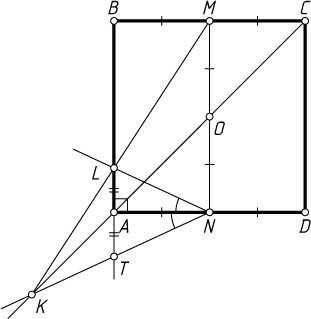
2307. Дан квадрат ABCD
, M
и N
— середины сторон BC
и AD
соответственно. На продолжении диагонали AC
за точку A
взяли точку K
. Отрезок KM
пересекает сторону AB
в точке L
. Докажите, что углы KNA
и LNA
равны.
Решение. Пусть прямые AB
и KN
пересекаются в точке T
. Поскольку отрезки MN
и AC
пересекаются в центре O
квадрата ABCD
, отрезок KO
— медиана треугольника KMN
, а так как TL\parallel MN
, то KA
— медиана треугольника KLT
. Значит, A
— середина LT
, а NA
— медиана и высота треугольника LNT
, поэтому треугольник LNT
равнобедренный. Следовательно, NA
— биссектриса угла LNT
. Что и требовалось доказать.
Источник: Турнир городов. — 2004-2005, XXVI, весенний тур, младшие классы, тренировочный вариант
