2309. Окружность \Omega_{1}
проходит через центр окружности \Omega_{2}
. Из точки C
на окружности \Omega_{1}
проведены касательные к \Omega_{2}
, вторично пересекающие \Omega_{1}
в точках A
и B
. Докажите, что отрезок AB
перпендикулярен прямой, проходящей через центры окружностей.
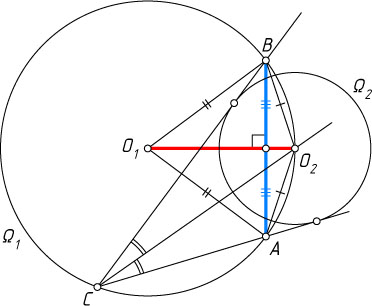
Решение. Рассмотрим случай, изображённый на рисунке. Центр O_{2}
окружности \Omega_{2}
, вписанной в угол ACB
, лежит на биссектрисе этого угла, значит, точка O_{2}
— середина дуги AO_{2}B
окружности \Omega_{1}
. Поэтому O_{2}A=O_{2}B
, т. е. точка O_{2}
равноудалена от концов отрезка AB
. Центр O_{1}
окружности \Omega_{1}
также равноудалён от концов этого отрезка. Следовательно, O_{1}O_{2}
— серединный перпендикуляр к отрезку AB
.
Аналогично для остальных случаев.
Примечание. Разбора отдельных случаев можно избежать, если рассматривать ориентированные углы.
Автор: Заславский А. А.
Источник: Московская математическая олимпиада. — 2005, LXVIII, 9 класс
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 3, с. 65
Источник: Турнир городов. — 2004-2005, XXVI, весенний тур, старшие классы, основной вариант
