2310. В треугольнике ABC
биссектриса угла A
, серединный перпендикуляр к стороне AB
и высота, опущенная из вершины B
, пересекаются в одной точке. Докажите, что биссектриса угла A
, серединный перпендикуляр к стороне AC
и высота, опущенная из вершины C
, также пересекаются в одной точке.
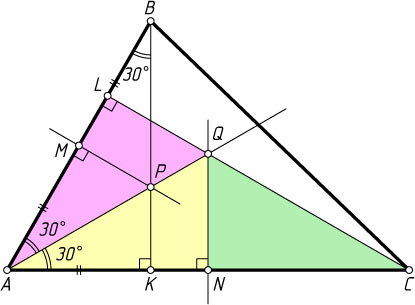
Решение. Пусть M
— середина стороны AB
, P
— точка пересечения биссектрисы угла A
, серединного перпендикуляра к стороне AB
и высоты BK
.
Прямоугольные треугольники APM
и APK
равны по гипотенузе и острому углу, поэтому AK=AM=\frac{1}{2}AB
. Катет AK
прямоугольного треугольника AKB
равен половине гипотенузы AB
, поэтому \angle BAK=60^{\circ}
.
Пусть Q
— точка пересечения серединного перпендикуляра к стороне AC
и высоты CL
, опущенной из вершины C
. Докажем, что точка Q
лежит на биссектрисе угла A
.
Действительно, точка Q
лежит на серединном перпендикуляре к отрезку AC
, значит, QA=QC
, т. е. треугольник AQC
равнобедренный. Из прямоугольного треугольника ACL
находим, что
\angle ACL=90^{\circ}-\angle CAL=90^{\circ}-60^{\circ}=30^{\circ}.
Значит,
\angle CAQ=\angle ACQ=\angle ACL=30^{\circ}=\frac{1}{2}\angle BAC.
Следовательно, точка Q
лежит на биссектрисе угла BAC
. Что и требовалось доказать.
Источник: Турнир городов. — 2003-2004, XXV, весенний тур, младшие классы, тренировочный вариант
