2311. Звенья AB
, BC
и CD
ломаной ABCD
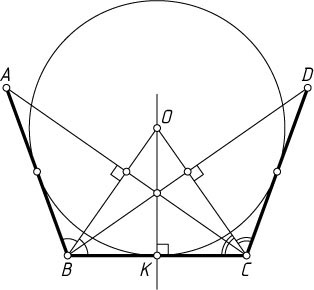
равны и касаются некоторой окружности с центром O
. Докажите, что точка K
касания этой окружности со звеном BC
, точка O
и точка пересечения прямых AC
и BD
лежат на одной прямой.
Решение. Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому BO
— биссектриса угла ABC
. Биссектриса равнобедренного треугольника ABC
является его высотой, поэтому OB\perp AC
. Аналогично OC\perp BD
. Радиус, проведённый в точку касания, перпендикулярен касательной, поэтому OK\perp BC
.
На прямых AC
, BD
и OK
лежат высоты треугольника BOC
, следовательно, эти прямые пересекаются в одной точке. Отсюда следует утверждение задачи.
Источник: Турнир городов. — 2003-2004, XXV, весенний тур, старшие классы, тренировочный вариант
