2312. Две окружности пересекаются в точках A
и B
. Их общая касательная (та, которая ближе к точке B
) касается окружностей в точках E
и F
. Прямая AB
пересекает прямую EF
в точке M
. На продолжении AM
за точку M
выбрана точка K
так, что KM=MA
. Прямая KE
вторично пересекает окружность, содержащую точку E
, в точке C
. Прямая KF
вторично пересекает окружность, содержащую точку F
, в точке D
. Докажите, что точки C
, D
и A
лежат на одной прямой.
Решение. По теореме о касательной и секущей ME^{2}=MB\cdot MA=MF^{2}
, значит, ME=MF
.
Диагонали четырёхугольника AEKF
точкой M
пересечения диагоналей делятся пополам, значит, AEKF
— параллелограмм, поэтому \angle EAF=\angle EKF
.
Пусть T
— точка на продолжении отрезка FE
за точку E
. Из теоремы об угле между касательной и хордой следует, что
\angle CAE=\angle CET=\angle KEF.
Аналогично \angle FAD=\angle KFE
.
Значит,
\angle CAE+\angle EAF+\angle FAD=\angle KEF+\angle EKF+\angle KFE=180^{\circ}
(сумма углов треугольника KEF
). Следовательно, точки C
, D
и A
лежат на одной прямой.
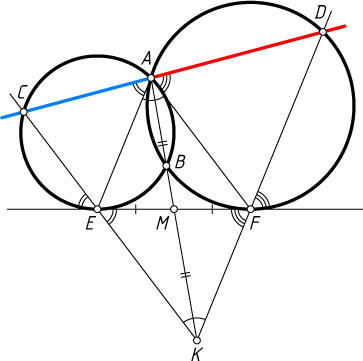
Автор: Макаров М. А.
Источник: Турнир городов. — 2003-2004, XXV, весенний тур, младшие классы, основной вариант
