2313. Внутри треугольника ABC
взята точка P
так, что угол ABP
равен углу ACP
, а угол CBP
равен углу CAP
. Докажите, что P
— точка пересечения высот треугольника ABC
.
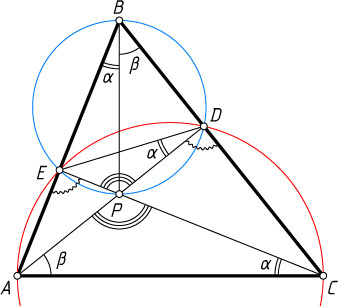
Решение. Первый способ. Пусть прямая AP
пересекает сторону BC
в точке D
, а прямая CP
пересекает сторону AB
в точке E
(рис. 1). Обозначим
\angle ABP=\angle ACP=\alpha,~\angle CBP=\angle CAP=\beta.
Тогда
\angle DPE=\angle APC=180^{\circ}-\alpha-\beta=180^{\circ}-\angle DBE,
значит, четырёхугольник BDPE
вписанный. Поэтому
\angle ADE=\angle PDE=\angle PBE=\alpha=\angle ACE.
Из точек D
и C
, лежащих по одну сторону от прямой AE
, отрезок AE
виден под одним и тем же углом, значит, точки D
, E
, A
и C
лежат на одной окружности. Вписанные в эту окружность углы ADC
и AEC
опираются на одну и ту же дугу, поэтому они равны. Следовательно,
\angle ADC=\angle AEC=180^{\circ}-\angle BEP=\angle PDB=\angle ADB.
Смежные углы ADC
и ADB
равны, значит, они прямые, т. е. AD
— высота треугольника ABC
. Аналогично CE
— также высота треугольника ABC
. Следовательно, P
— точка пересечения высот этого треугольника.
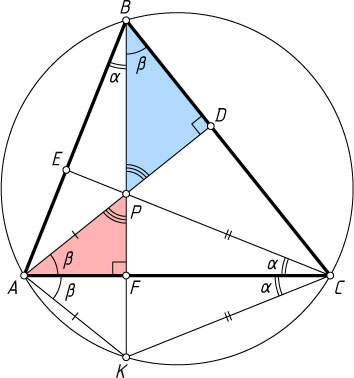
Второй способ. Пусть прямая CP
пересекает сторону AB
в точке E
, прямая BP
пересекает сторону AC
в точке F
, а описанную окружность треугольника ABC
— в точке K
(рис. 2). Обозначим
\angle ABP=\angle ACP=\alpha,~\angle CBP=\angle CAP=\beta.
Вписанные углы CAK
и CAP
опираются на одну и ту же дугу, поэтому
\angle CAK=\angle CBK=\angle CAP=\beta=\angle PAC.
Аналогично \angle ACP=\angle ACK
. Тогда треугольники CAK
и CAP
равны по стороне и прилежащим к ней углам, поэтому AK=AP
. Биссектриса AF
равнобедренного треугольника является его высотой, поэтому BF
— высота треугольника ABC
.
Два угла треугольника AEC
соответственно равны двум углам треугольника AFB
, значит, их третьи углы также равны, т. е. \angle AEC=\angle AFB=90^{\circ}
. Поэтому CE
— высота треугольника ABC
. Следовательно, P
— точка пересечения высот этого треугольника.
Автор: Женодаров Р. Г.
Источник: Турнир городов. — 2002-2003, XXIV, осенний тур, младшие классы, основной вариант

